Home
 

Implementando fibonacci em Haskell

por Pedro Tacla Yamada

A mágica da avaliação não estrita e funções de alta ordem. Um crash course de 5 minutos em Haskell e a descontrução da implementação de fibonacci clássica em uma linha com comparações de trechos de JavaScript.

Muitos que se aventuraram em aprender Haskell devem ter se deparado com a implementação da sequência de Fibonacci em uma linha e com complexidade linear. Vamos a desconstruir, já que isso ainda não foi feito em português.

Haskell em 5 minutos

Haskell é uma linguagem de programação funcional, não estrita, pura e fortemente “tipada”. Isso quer dizer que é uma linguagem onde funções são membros de primeira ordem, onde a avaliação é “lazy” por padrão, onde o IO do programa precisa estar isolado da lógica, sem loops, sem variáveis e onde todos os valores tem tipos (o compilador reclama quando algo não faz sentido). A ausência de loops e variáveis é contornável de duas formas:

Operando com números

Em JavaScript:

// "//" é um comentário
1 + 10 // => 11
2 * 3  // => 6

Em Haskell:

-- "--" é um comentário
1 + 10 -- => 11
2 * 3  -- => 6

Operando com listas

Em JavaScript:

[1, 2, 3, 4] // => [1, 2, 3, 4]
[1, 2]       // => [1, 2]
[1, 2][0]    // => 1
[1, 2][1]    // => 2

Em Haskell:

[1, 2, 3, 4] -- => [1, 2, 3, 4]
[1, 2]       -- => [1, 2]
[1, 2] !! 0  -- => 1
[1, 2] !! 1  -- => 2

-- Adicionando um elemento na frente da lista (haskell-only):
1 : [2, 3]   -- => [1, 2, 3]

Condicionais

Em JavaScript:

if(something) {
  // ...
} else if(somethingElse) {
  // ...
} else {
  // ...
}

Em Haskell:

if something
    then -- ...
    else if somethingElse
        then -- ...
        else -- ...

Definindo funções

Em JavaScript:

function soma10(numero) { return numero + 10 }
function elevaAoQuadrado(numero) { return numero * numero }

Em Haskell:

soma10 numero = numero + 10
elevaAoQuadrado numero = numero * numero

Usando funções

Em JavaScript:

soma10(2)           // => 12
elevaAoQuadrado(10) // => 100

Em Haskell:

soma10 2           -- => 12
elevaAoQuadrado 10 -- => 100
Paralelo com a biblioteca lodash

A biblioteca lodash tem uma série de funções com equivalentes no Haskell. Algumas que valem a pena mencionar:

Por que digo “listas” e não Arrays?


Em Haskell, por padrão, o literal [1, 2, 3] é uma “lista” e não um Array. Isso quer dizer que quando escrevo [1, 2, 3] estou denominando a estrutura de dados “lista ligada”. Ou seja uma lista é um elemento e uma referência para uma outra lista com o resto da lista (!). Em JavaScript:

var vazia = {};

function lista(x, resto) {
  return { primeiro: x, resto: resto, };
}

function primeiro(lista) { return lista.primeiro; }
function resto(lista) { return lista.resto; }

function index(lista, n) {
  if(lista === vazia) return null;
  else if(n === 0) return lista.primeiro;
  else return index(lista.resto, n - 1);
}

function length(lista) {
  var len = 0;
  while(lista !== vazia) {
    len += 1;
    lista = lista.resto;
  }
  return len;
}

Construímos [1, 2, 3] com:

lista(1, lista(2, lista(3, vazia)));

Note que isso é equivalente ao uso do : em Haskell:

1 : 2 : 3 : []

Na verdade o : pode ser considerado como um sugar para algo equivalente a lista em JavaScript e o [] um alias para algo equivalente a vazia no código acima. Podemos inclusive definir isso, apesar de que entrar nos detalhes de definição de operadores ou estruturas de dados não é o intuito desse post:

vazia = []
lista x resto = x : resto

E usar nossas definições

lista 1 (lista 2 (lista 3 vazia))
Algumas propriedades dessa característica

Avaliação preguiçosa

Uma das coisas fundamentais do Haskell é a avaliação preguiçosa. No fundo, Haskell é uma linguagem de boa. Ela não faz nada que não precisa. Então quando se escreve:

let x = soma10 200

O nome x se refere a computação soma10 200 e não seu resultado. Quando precisamos do valor (seja para imprimir no console ou mandar como uma resposta HTTP) é que ele e todos os valores dos quais depende são computados.

Algo parecido agora faz parte da popular biblioteca lodash para o JavaScript. Quando chamo:

var numerosPrimosAte100 = _(_.range(0, 100)).filter(ehPrimo);

Nada acontece. Somente quando numerosPrimosAte100.value() é chamado que a computação ocorre. Isso abre portas para programas em estilo funcional com mais expressividade sem desperdiçar iterações. No caso de Haskell abre portas para listas infinitas. A notação de ranges usando lodash e Haskell:

_.range(0, 5)
// => [0, 1, 2, 3, 4]
_.range(0, 10, 2)
// => [ 0, 2, 4, 6, 8 ]
// de 0 a 9 com 2 de intervalo

E em Haskell:

[0..4]
-- => [0, 1, 2, 3, 4]
[0,2..9]
-- => [0, 2, 4, 6, 8]
-- de 0 a 9 com 2 de intervalo
-- (basta escrever [n1, n2, n3..nLimite])

E porque a linguagem é lazy, podemos bem fazer:

[0..]
-- => [0, 1, 2, 3, 4, 5, 6, ...]

Se tentarmos imprimir isso, o programa não acaba nunca de escrever números na tela. Mas se armazenarmos em um nome, podemos operar sobre a lista sem problemas. Um exemplo usando o operador !! para acessar o 10 número dessa sequência infinita:

let x = [0..]
print (x !! 10) -- => 10

Implementando fibonacci

A sequência de fibonacci é definida pela Wikipédia como:

uma sequência de números inteiros, começando normalmente por 0 e 1, na qual, cada termo subsequente (número de Fibonacci) corresponde a soma dos dois anteriores

Como uma fórmulinha:

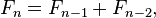
Uma implementação ingênua imperativa JavaScript:

function fibonacci(len) {
  var ret = [0, 1];
  for(var i = 2; i < len; i++) {
    ret[i] = ret[i - 1] + ret[i - 2];
  }
  return ret;
}

fibonacci(5); // => [ 0, 1, 1, 2, 3 ]

Digo ingênua só porque calcular fibonacci(10) e em seguida fibonacci(100) não reutiliza resultados existentes.

Olhando para a lista

Podemos pensar em todos os elementos menos os dois primeiros da lista, como sendo todos os elemtos da lista somados a todos os elementos menos o primeiro elemento da lista.

wat?

Veja só, pense que temos uma lista infinita:

fibs = 0 : 1 : restoDeFibs

Se isso já estivesse computado, poderíamos pensar em:

fibs -- => 0, 1, 1, 2, 3, 5, ...

E se pensarmos em todos os elementos menos o primeiro de fibs; o resultado de tail fibs:

fibs      -- => 0, 1, 1, 2, 3, 5, ...
tail fibs -- => 1, 1, 2, 3, 5, 8, ...

Não sei se é fácil de enxergar isso, mas tail (tail fibs) é:

fibs             -- =>  0     ,  1     ,  1     ,  2     ,  3     ,  5     , ...
tail fibs        -- =>      1 ,      1 ,      2 ,      3 ,      5 ,      8 , ...
tail (tail fibs) -- => (0 + 1), (1 + 1), (1 + 2), (2 + 3), (3 + 5), (5 + 8), ...
tail (tail fibs) -- =>    1   ,    2   ,    3   ,    5   ,    8   ,    13  , ...

A lista fibs é definida como 0 : 1 : (somaDasListas fibs (tail fibs))! Nosso restoDeFibs é igual a somaDasListas fibs (tail fibs).

O que nos leva a função somaDasListas. Para todos os elementos na lista 1, soma o mesmo elemento da lista 2. A implementação clássica usa a função zipWith que tem um equivalente no lodash _.zipWith. Vamos precisar de outra função chamada null que retorna true se a lista estiver vazia. A ideia é dada uma função fn, uma lista1 e uma lista2 aplicamos fn elementoDaLista1 elementoDaLista2 para todos os elementos das listas (supondo que tenham o mesmo tamanho) e retornamos uma lista com os resultados. Então:

zipWith fn lista1 lista2 =
    -- Se lista1 ou lista2 são vazias, retornamos a lista vazia:
    if (null lista1) || (null lista2)
        then []
        -- Senão retornamos `fn` aplicado ao primeiro elemento de cada lista e
        -- `zipWith fn` aplicado ao resto de cada lista
        else (fn (head lista1) (head lista2)) :
             zipWith fn (tail lista1) (tail lista2)

Com tudo isso. Podemos escrever fibonacci como:

fibs = 0 : 1 : zipWith (+) fibs (tail fibs)

Declaramos uma lista infinita definida em termos dela mesma! E podemos a usar com:

fibs !! 10 -- => 55

Amarrando as pontas

Se você chegou até aqui, obrigado. Muito desse post tentou ser o mais simples possível para pessoas que nunca viram Haskell, então não, isso não é como Haskell se parece em produção. Mesmo assim, é divertido ver o que é possível com a linguagem e talvez isso tenha te animado para a estudar.

Esse foi o primeiro post do blog da HaskellBR. Dúvidas comentários e posts são aceitos no repositório do GitHub: https://github.com/haskellbr/blog. No momento a meta é ter conteúdo publicado semanalmente.

Share Comente no Twitter